In the field of statistics and data analysis, comparing means is a frequent endeavor—whether that means testing the effectiveness of a new drug or analyzing average student scores before and after a training program. In reaching these means accurately, analysts typically use two tests — the Paired t-test and the Unpaired t-test.
Although both compare means, they are used in completely different situations. Let’s understand what they are, how they differ, and when to use each.
What Is a T-Test?
A paired t-test, or dependent sample t-test, is a statistical technique employed to assess the difference between the means of two groups that are somehow related.
Commonly, paired t-tests are applicable when we measure the same subjects on two separate occasions – for instance, before and after some treatment – or when the two observations are linked in some natural order, such as measurements obtained from twins, matched pairs, or two different conditions imposed on a single subject.
It helps verify if an observed difference is due to chance or a real effect.
There are two major types:
-
Paired (Dependent) t-test
-
Unpaired (Independent) t-test
What Is a Paired T-Test?

A Paired t-test is used when the two samples are related or dependent on each other.
You use it when:
-
The same group is tested twice (before and after treatment).
-
The data points are naturally paired (e.g., left vs right eye, twin studies).
🔹 Formula:
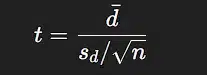
Where:
-
dˉ = mean of the differences between pairs
-
sd = standard deviation of differences
-
n = number of pairs
🔹 Example:
A teacher wants to check if a new teaching method improved scores.
She compares before and after scores of the same 10 students.
Because it’s the same group, this is a paired test.
What Is an Unpaired T-Test?

An Unpaired t-test, also called an Independent Samples t-test, is used when the two samples are unrelated.
You use it when:
-
You are working with two separate groups of subjects.
-
Each group of subjects was tested just once, under different conditions.
Formula:
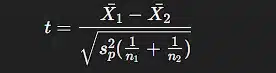
Where:
-
X1ˉ, X2ˉ = sample means
-
sps_psp = pooled standard deviation
-
n1, n2 = sample sizes
Example:
A researcher compares the average height of boys and girls in a class.
Since they are two different groups, this is an unpaired test.
Paired vs Unpaired T-Test: Key Differences
| Feature | Paired T-Test | Unpaired T-Test |
|---|---|---|
| Data Type | Related / Dependent | Unrelated / Independent |
| Example | Same subjects before & after treatment | Two different groups |
| Purpose | Measures change within a group | Compares two separate groups |
| Sample Relation | Dependent | Independent |
| Formula | Mean of differences | Difference between means |
| Variance | Uses differences only | Pooled from both groups |
| Typical Use | Pre-test vs post-test | Control vs treatment groups |
When to Use Paired vs Unpaired Tests
Use Paired T-Test when:
-
Have the same participants measured twice
-
Are comparing matched pairs (i.e twins, left/right hand)
-
Conduct a “before-after” study design
Use Unpaired T-Test when:
-
Test two separate groups once each
-
Do not have any natural pairing
-
Are comparing performance between two completely independent groups
Real-World Examples
Example 1 – Paired Test:
A dietitian measures patient weight before and after a diet plan.
→ Same subjects → Paired T-Test.
Example 2 – Unpaired Test:
A company is examining productivity between remote and office employees.
→ Two different groups → Unpaired T-Test.
Assumptions for Both Tests
-
The data is continuous (interval-ratio scale).
-
The data is normally distributed
-
The variance is similar.
-
The observations are randomly selected.
For Paired tests, differences should also follow normality.
How to Perform a T-Test in Python
Here’s a quick example using scipy.stats:
xml
from scipy import stats
# Paired test
before = [70, 68, 75, 80, 72]
after = [75, 70, 78, 82, 74]
t_stat, p_value = stats.ttest_rel(before, after)
print("Paired test p-value:", p_value)
# Unpaired test
group1 = [10, 12, 14, 13, 15]
group2 = [8, 9, 7, 10, 6]
t_stat2, p_value2 = stats.ttest_ind(group1, group2)
print("Unpaired test p-value:", p_value2)Common Mistakes to Avoid

-
Using a paired test for independent data
-
Forgetting to check assumptions of normality
-
Ignoring outliers that distort means
-
Not reporting p-values properly
Always verify whether your groups are dependent or independent before choosing the test.
Conclusion
Both the paired and unpaired t-tests are important ways to make a statistical comparison. A paired test helps make sense of change in the same group, while the unpaired means compares the difference between separate groups.
Choosing the correct test ensures valid results and avoids misleading conclusions — the golden rule:
Same subjects = Paired test, Different subjects = Unpaired test.
FAQs
1. How to choose between a paired and unpaired t-test?
To decide whether to use a paired or unpaired t-test, start by checking the relationship between your two datasets:
-
Use a paired t-test if the samples are related — meaning the same subjects are measured twice (e.g., before and after treatment) or naturally matched pairs (e.g., twins, left vs right eye).
-
Use an unpaired t-test if the samples are independent, such as comparing two different groups of people (e.g., male vs female heights).
2. Which test should I use for before-after studies?
Use a paired t-test, as the data involves the same participants.
3. Can I use the unpaired t-test for dependent samples?
No, it would produce incorrect results; always match test type to data relationship.
4. What does the p-value indicate?
It shows whether the observed difference between means is statistically significant.
5. Which software can perform these tests?
Python (SciPy), R, SPSS, Excel, and Keploy (for API data-driven tests) can all be used.


Leave a Reply